# 0X00 前言
前面两篇文章算是大概概括了比特币的基本概念,从本期开始,我就逐步展开细节知识,我会继续深入浅出的讲解,小白可以跳着读。
大多数人都知道区块链的数据不可篡改,写入比特币区块链上的数据当然也是不可篡改逆转的,但是很多人却误以为比特币是一成不变的,而实际上比特币是在持续更新的。
突然想起件事情,经常听到有人说量子计算机可以摧毁比特币,如果量子计算机目的是摧毁整个密码学,那么当前计算机所依赖的一切密码学安全性将荡然无存,人类的网络生活将陷入混乱,所以正常的逻辑应该是:量子计算成熟之时,建立在量子计算之上的密码学必然也应运而生或者说可以抵抗量子计算机的密码学也将被广泛应用,所有建立于密码学的安全协议将会升级,当然包括开发非常活跃的比特币;
另外懂点密码学的都知道其背后的理论依据是各种数学难题,量子计算机如果能解决所有数学难题,人类岂不是可以掌握宇宙中的所有秘密了,彼时,国家宗教将都失去意义,人类了脱生死,到达终点。。。
所以比特币有一百种死法,但是应该轮不到量子计算机。
回到正文,下面我们就以小见大,从比特币的地址类型和交易类型去了解比特币的不断发展更新。
# 0X01 比特币公私钥基础
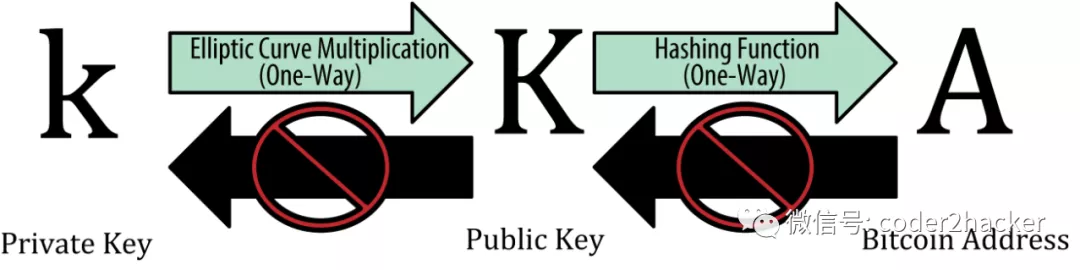
首先我们先搞清楚一下比特币的地址(BTC Address)、公钥(Public Key)、私钥(Private Key)的关系
简单来说就是下图所示,从私钥小k生成公钥大K,从公钥大K再生成比特币地址A,整个过程不可逆,即不可反推。
可见,比特币的安全性也是建立在目前的公钥基础设施之上的,最关键的是从私钥单向得到公钥,至于公钥和地址之间的单向关系倒不是多么重要(如果我说错请指正),因为公钥总归是会暴露给网络的(比如比特币交易最基本的 <Sig><PubKey>解锁脚本)
 暂时抛开 地址(BTC Address) 先来说说比特币的公私钥是如何生成的
暂时抛开 地址(BTC Address) 先来说说比特币的公私钥是如何生成的
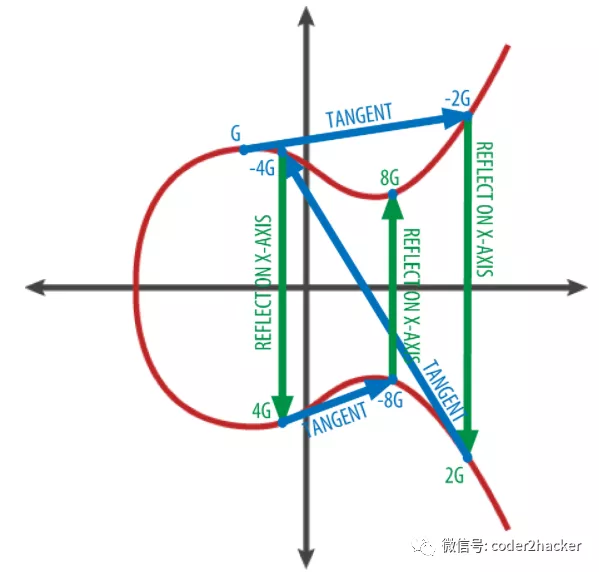 上图的曲线就是ecc椭圆曲线方程所对应的图像:
y2 = x3 + ax + b mod p
上图的曲线就是ecc椭圆曲线方程所对应的图像:
y2 = x3 + ax + b mod p
然后图中的G(Generator)是一个指定的初始起点,然后从这个点开始做切线,切线和曲线的交点画垂线,垂线跟曲线的交点就是2G,然后继续重复就可以走到4G、8G等位置,
那么3G呢?
3G=G+2G,两个点的"加法"定义为,在图中连线两个点,直线和曲线的交点向X轴画垂线,垂线跟曲线的交点即为结果,
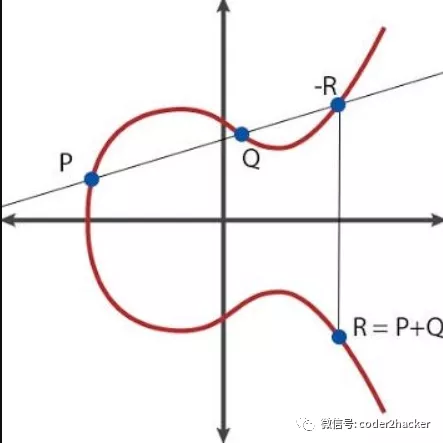 综上所述,表示为:
综上所述,表示为:
K=k*G
当然这里的* 不是通常的乘法,而是前面定义的"加法"的一种表示, 你可能好奇,为什么在曲线上定义这么奇怪的计算方法,数学或密码学专业的朋友可能觉着小儿科,对于不懂的朋友不用急,你先简单记着这是一种所谓有限循环群 finite cyclic group 的计算定义,我后续会继续编写基础文章,这里不做展开
然后我们将小k作为私钥,大K作为公钥,
,当然可能你直观的觉着,知道了公钥大K,好像应该很容易得到私钥小k,不要被这里的1 2 3 误解,实际的私钥是32个字节256位,所以比特币的私钥空间大小是 2^256,这是个相当惊人的数字,大概是十进制的10^77,我们已知可见的宇宙中原子总数大概是 10^80个。
如果小白还是找不到感觉,我再举几个例子:
常用的RSA密码算法是基于大数分解素数问题;
常见的安全连接握手使用的DH密钥交换是基于离散对数问题;
一个数字的分解,一个对数的计算,小学生都会做,6可以分解为2和3,lg10=1,但是涉及到大数,这些都是数学难题,尤其随着私钥的长度增加(数字范围变大),基于现有破解手段在当前的普通计算机上破解需要消耗的时间越长,密码学的安全性也基于此,刚才也说了,即使量子计算机出来,基于量子计算机的密码学也会有成熟的安全方案。
# 0X02 私钥的细节
私钥本质就是选择1到2^256之间的一个随机数,更准确地说,私钥可以是[0, n-1]之间的任何数字,其中n = 1.1578 * 10^77,略小于2^256,n就是比特币所使用的椭圆曲线的阶数,所以我们随机选择一个256位的数字,并检查它是否小于n。
生成私钥最重要的就是增加熵值或使用安全的随机值,只要是不可预测的或重复的就可以,比特币软件使用底层操作系统的随机数生成器来产生256位的熵(随机性)。通常操作系统随机数生成器是由人为的随机性源来初始化的,所以这就是为什么系统可能会要求您动几秒钟鼠标的原因。
再具体点说下生成方法,通常就是将从安全的随机性源中收集的更大的随机位串(a larger string of random bits)输入到SHA256哈希/散列算法,SHA256散列算法将生成256位的数字,如果结果小于n,则我们就得到了一个合适的私钥,否则只需使用另一个随机数再试一次。
注意:
- 不要写自己的代码来生成随机数字;
- 如果非要自己写,也千万不要使用编程语言默认的基础库提供的简单的随机生成器,要使用安全的密码学伪随机数字生成器(CSPRNG - cryptographically secure pseudorandom number generator),并使用具有足够的熵值的来源(比如鼠标的随机滑动);
- 如果需要更好的安全保证,那么就得好好研究下所选用的 CSPRNG 实现方法或者其文档,以确保该方法是足够安全的。
- 尽量不要随便使用网上的在线生成器,原因参考《比特币在线生成器后门》 (opens new window),如果非要使用,尽量选择公开源码的,将源码下载下来离线生成;
举例, 使用bicoin-cli:
# 生成比特币地址
lyhistory@lyhistory-VirtualBox:/opt/bitcoin$ ./src/bitcoin-cli createwallet "test"
lyhistory@lyhistory-VirtualBox:/opt/bitcoin$ ./src/bitcoin-cli -rpcwallet="test" getnewaddress test01
lyhistory@lyhistory-VirtualBox:/opt/bitcoin$ ./src/bitcoin-cli -rpcwallet="test" getaddressesbylabel "liuyue01"
2NDHhHaxH9gRFGNxT4seonVq2Unroz
# 获取公钥信息(通常普通用户不需要知道公钥信息,只需要地址和私钥即可)
lyhistory@lyhistory-VirtualBox:/opt/bitcoin$ ./src/bitcoin-cli -rpcwallet="test" getaddressinfo "2NDHhHaxH9gRFGNxT4seonVq2Unroz"
# 获取私钥
lyhistory@lyhistory-VirtualBox:/opt/bitcoin$ ./src/bitcoin-cli -rpcwallet="test" dumpprivkey 2NDHhHaxH9gRFGNxT4seonVq2Unroz
使用python脚本:
# Install Python PIP package manager
$ sudo apt-get install python-pip
# Install the Python ECDSA library
$ sudo pip install ecdsa
# Run the script
$ python ec-math.py
Secret: 38090835015954358862481132628887443905906204995912378278060168703580660294000
EC point: (70048853531867179489857750497606966272382583471322935454624595540007269312627, 105262206478686743191060800263479589329920209527285803935736021686045542353380)
BTC public key: 029ade3effb0a67d5c8609850d797366af428f4a0d5194cb221d807770a1522873
但是这里使用了 os.urandom,它反映了底层操作系统提供的加密安全随机数生成器(CSRNG),但是 注意:视操作系统而定,os.urandom的实现方式可能没有足够的安全,所以可能不适用于真正的product生产环境。
讲完了生成方法,最后说下私钥的呈现方式
私钥是 256字节数字,其在比特币代码内部通常是由 raw二进制或者hex格式表示,而对于外部软件或用户来说通常会进行格式化,比如将其base58编码为所谓的“钱包导入格式” (WIF- wallet import format) 以方便在不同的钱包直接导入导出,另外现在还有流行的二维码的呈现方式;
# 0X03 公钥的细节
不知道前面大家有没有注意到计算出的公钥大K好像是个位于椭圆曲线上的坐标点(x,y),这怎么玩?
答案是:没有经过压缩的公钥还真是由(x,y)组成的(前面再加个0x04前缀),x和y都是32个字节256位,加上前缀,一共65字节520位,岂不是很长,对的,0x04前缀就是为了跟下面的压缩后的公钥区分的:
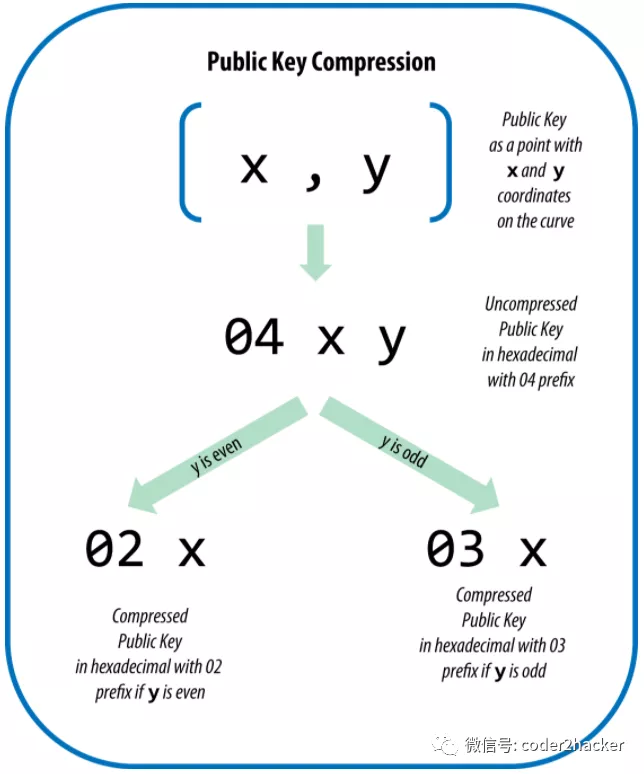 引入压缩公钥的目的就是为了减少比特币交易的大小从而节省保存了比特币区块链数据库的节点上的磁盘空间(一个为压缩公钥就是520位,一个区块有数百个交易,再加上每天无数的交易,将会占用的磁盘空间),大多数交易都是包含公钥的(大多数交易都是所谓的P2PKH,公钥是用于验证某个比特币使用者的身份)。
引入压缩公钥的目的就是为了减少比特币交易的大小从而节省保存了比特币区块链数据库的节点上的磁盘空间(一个为压缩公钥就是520位,一个区块有数百个交易,再加上每天无数的交易,将会占用的磁盘空间),大多数交易都是包含公钥的(大多数交易都是所谓的P2PKH,公钥是用于验证某个比特币使用者的身份)。
我们回头看下上面的椭圆曲线图,知道了 x 坐标,貌似可以得到两个 y 坐标,一个正一个负,所以只要能保存 y 坐标的正负,再加上x坐标,就可以得到y坐标了,做法就是:
When calculating the elliptic curve in binary arithmetic on the finite field of prime order p, the y coordinate is either even or odd, which corresponds to the positive/negative sign as explained earlier.
Mastering Bitcoin
大概意思就是, 使用二进制来计算 阶数为素数p的有限域的椭圆曲线函数时,正负可以用奇数偶数来对应,具体的数学上的原理,我没有深入研究,初步的理解就是因为二进制本身只是0和1,所以为了表示负数是需要进行补位等各种操作,可能刚好在素数p阶的椭圆函数有限域,椭圆曲线上某个x坐标对应的正负y,其二进制分别是奇数或偶数,刚好可以区分,所以就使用前缀 0x02 代表奇数,0x03代表偶数,举个不恰当的例子:
这里纯粹是假设性的举例以帮助理解,不能作为验证或证明
假设p=2
y=5 二进制:00101
二进制平方的十进制值=25 mod 2 = 1
y=-5 二进制:11010
二进制平方的十进制值=676 mod 2= 0
# 0X04 比特币地址-P2PKH
public key hash是最常见的一种类型的比特币地址,public key公钥就是前面讲的公钥,对其进行哈希计算就能得到比特币地址;
而P2PKH - pay to public key hash,意思就是 支付给比特币地址;
为什么要起个 P2PKH 这么奇怪的名字,因为可以说中本聪初原本只设计了包括P2PKH在内的不多的几种交易类型,然后后来大家对比特币进行扩展,比较重大的突破就是引入了P2SH - pay to script hash,让比特币具有了“智能合约”的能力,对于普通用户来说使用最多的就是P2PKH,这也是目前为止,比特币区块中比存在的比较多的交易类型;
所以后面如果看到我说 public key/pubkey hash或者P2PKH或P2PKH地址都是指的同一个东西,对于普通的比特币个人用户来说,我们安装比特币钱包(先抛开选择使用特殊的隔离见证segwit钱包功能)或者使用命令行,都会根据我前面说的规则生成公私钥,然后从公钥再进行哈希生成地址,然后这个地址就是常见的数字1开头的比特币地址; 具体怎么生成的呢:
pubkey hash
= HASH160
= RIPEMD160(SHA256(pubkey))
pubkey hash address
=Base58(pubkey hash)
=Base58(HASH160)
=Base58(RIPEMD160(SHA256(pubkey)))
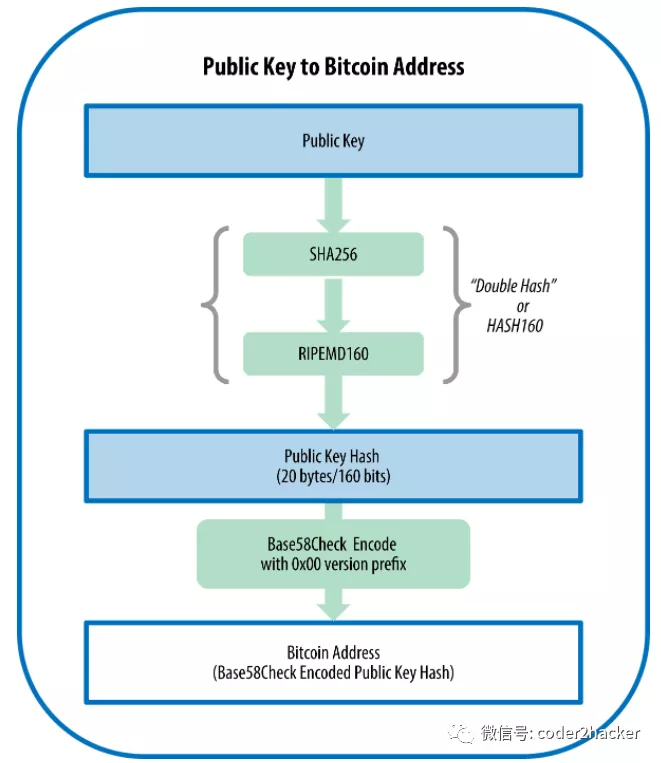
比特币地址基本上都是会用 Base58Check 进行编码(例外如segwit隔离见证地址),就是使用 base58 字符集 和 checksum增强可读性,避免歧义并防止地址转录和输入错误,不只是比特币地址,实际上比特币中需要人工地址转录或输入的很多地方都是用base58,比如私钥、加密密钥、脚本哈希。
具体原理:
 为了用紧凑的方式利用较少的字符表示长数字,很多计算机系统采用大于10的基数的混合字母数字表示,比如十六进制包括A到F,base64采用26个小写字母+26个大写字母+10个数字+2个字符符号(+/‘,不要误会=是作为padding)来通过基于文本的媒介来传输二进制,
为了用紧凑的方式利用较少的字符表示长数字,很多计算机系统采用大于10的基数的混合字母数字表示,比如十六进制包括A到F,base64采用26个小写字母+26个大写字母+10个数字+2个字符符号(+/‘,不要误会=是作为padding)来通过基于文本的媒介来传输二进制,
补充知识点:
很多人误以为计算机传输不应该都是二进制的吗,当然这个要看具体的场景和你的上下文语义,
我这里说的是在指的数据载荷 payload,通常来说,由于网络上设备众多,为了避免有些设备
可能会误将某些二进制作为控制字符来理解,所以将需要传输的数据载荷通过base64编码转换
再传输,网络设备就会将其当作文本,实例:
多数的加密数据,比如证书内容多采用base64编码;
当我们传输json数据的时候,由于json默认不支持二进制,如果需要装载二进制也通常要base64
编码,如果你使用unicode编码会很麻烦,因为会跟json的格式字符冲突;
当通过url传输二进制数据时,通常也是先base64编码,然后再urlencode(因为base64包含的+/对于url是特殊字符)
而作为base64的子集的base58则是用于包括比特币在内的多数加密货币的一种基于文本的二进制编码,base58不仅考虑了紧凑性,还有错误检测和预防,base58去除了一些容易在某些字体下看起来相同的数字和字符(数字0、大写字母O,小写字母l,大写字母I和符号(+/),base58字符集:
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
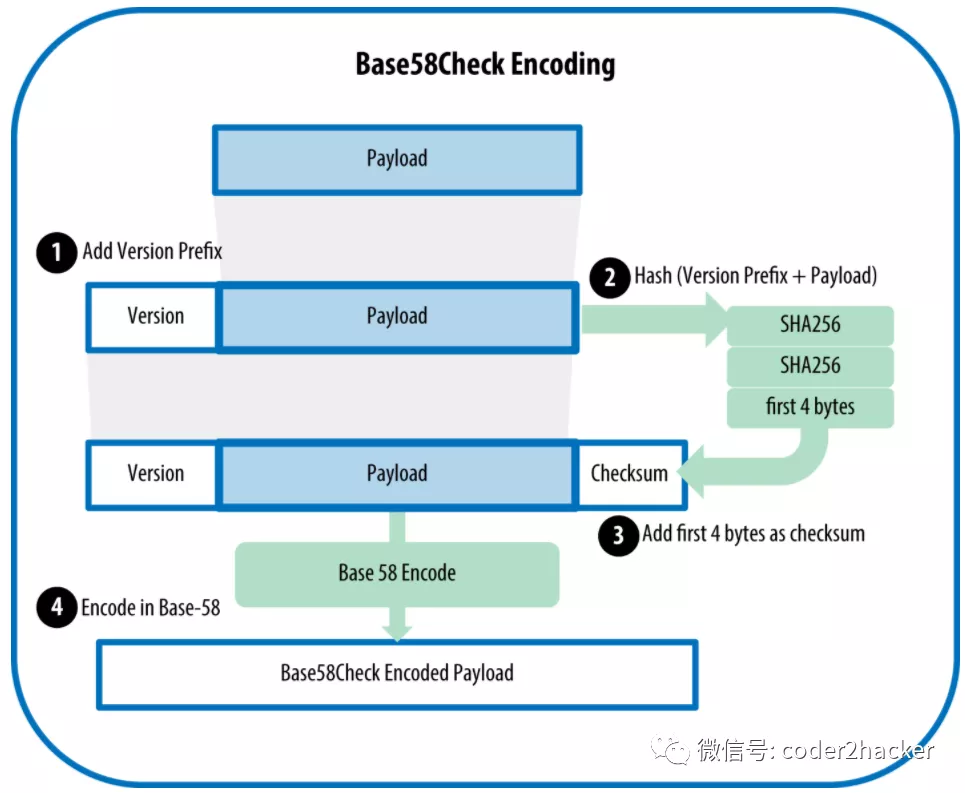
Base58Check就是一种Base58编码格式,多了数据尾部的4个字节作为内置的错误检查代码checksum,
checksum校验来自编码数据的哈希值,钱包软件的解码程序会从数据计算checksum并进行比较,这样可以防止钱包软件将输入错误的比特币地址作为有效目的地,否则会造成损失(往一个任何人都不拥有私钥的地址发送比特币可以叫做比特币销毁)。
那钱包软件如何知道这个格式是 Base58Check呢,我们需要在数据前面加个 version prefix,比如我们本文讲解的常见的P2PKH 类型的比特币地址默认的前缀是采用 0x00,其对应的私钥编码的前缀是 0x80,其他比特币地址和私钥类型及前缀,下文再继续讲解,现在我们先大概看下有哪些类型:
| 类型 | 版本前缀(hex) | 编码类型 | 编码后的前缀 |
|---|---|---|---|
| Pay-to-PublicKey-Hash Address | 0x00 | Base58 | 1 |
| Bitcoin Testnet Address | 0x6F | Base58 | m or n |
| Pay-to-Script-Hash Address | 0x05 | Base58 | 3 |
| BIP-32 Extended Public Key | 0x0488B21E | Base58 | xpub |
| segwit | no version prefix | Bech32 | bc1 |
注意到,上面我高亮了第二行 Testnet地址,这个是指跟比特币主网 mainnet不同的一个公开的测试网,就是说普通人或开发者可以在testnet上面做各种测试,当然testnet上面的不是真正的比特币,所以加上前缀0x6F,用于让钱包可以区分开主网地址和测试网地址,以防用户不小心将比特币转入测试网地址。
私钥类型
为了配合前面说的公钥的压缩,私钥这里也需要“压缩”,实际上这里的“压缩”只是为了字面上配合公钥的压缩,实际上不但没压缩,反而是增加了字符,就是为了让钱包知道这个私钥对应的公钥是经过压缩的
| 类型 | 版本前缀(hex) | Base58 编码后的前缀 |
|---|---|---|
| Private key (WIF, uncompressed pubkey) | 0x80 | 5 |
| Private key (WIF, compressed pubkey) | 0x80(加上后缀0x01) | K, or L |
| BIP32 Extended Private Key | 0x0488ADE4 | xprv |
| BIP-38 Encrypted Private Key | 0x0142 | 6P |
温故而知新,理解了上面的这些知识,最后再来温习下前面介绍过的最基本的比特币交易P2PKH的脚本,你会发现非常容易理解了:

解锁脚本/输入 scriptSig:<Sig><PubKey>
锁定脚本/输出 scriptPubKey:OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG
脚本执行顺序:
OP_DUP(PubKey)=PubKey duplicate复制 PubKey
OP_HASH160(PubKey) = PubKeyHash 得到PubKey的哈希即地址
OP_EQUALVERIFY(PubKeyHash,pubKeyHash)==TRUE 对比锁定脚本和从签名脚本生成的哈希地址是不是相同
OP_CHECKSIG(Sig, PubKey)==TRUE 最后检查签名 (PS.抱歉,前面有一篇文章介绍时漏了参数PubKey)
成功则验证了属于该签名拥有者的的比特币,并将生成一笔新的交易
参考资料
https://lyhistory.com/docs/blockchain/btc/btc_payment_integrate.html#_1-3-%E5%B7%A5%E4%BD%9C%E6%B5%81%E7%A8%8B
https://lyhistory.com/docs/blockchain/btc/btc_dev.html#_3-3-keys-addresses
https://lyhistory.com/docs/blockchain/btc/btc_bip.html#product-concern
https://wiki.openssl.org/index.php/Elliptic_Curve_Cryptography
https://en.wikipedia.org/wiki/Quadratic_residue#Prime_or_prime_power_modulus
https://bitcoin.stackexchange.com/questions/41662/on-public-keys-compression-why-an-even-or-odd-y-coordinate-corresponds-to-the-p
https://www.tutorialspoint.com/negative-binary-numbers