随着逐渐深入，可能大家注意到我之前“漏掉”了一个关键的知识链条，就是 签名Signature 的生成，签名的目的是证明你拥有该私钥，普通软件中签名是证明你是该信息或文档的拥有者，而对于不比特币来说，签名是证明你是这笔资金的拥有者，即你有权限使用该私钥控制的资金,

所以我现在有必要对比特币用到的椭圆曲线函数 ecc以及相应的签名算法 ecdsa 展开讲解，同时我会讲解一个实例，就是应alphawallet CTO 张韡武学长的邀请开发的一个小工具：express of trust address (opens new window)

Digital Signature

数字签名,又称公钥数字签名,是一种用于验证数字消息或文档的真实性的数学方案,具体来说是对消息或者文档的digest摘要进行签名计算生成的数字，有效的数字签名具有以下属性 ：

• 完整性 integrity

  保证该消息在传输过程中没有发生更改，简单的说就是如果消息被更改，则签名失效；

  对于比较长的消息或大的文档来说，通常需要对其先进行压缩 通常是进行哈希方法 Hash Function获取哈希值作为可以代表该消息或文档的message digest又称为指纹 fingerprint ，然后对哈希值进行签名，这里选用的哈希函数需要具备以下属性：

  • Arbitrary message size h(x) can be applied to messages x of any size.

  • Fixed output length h(x) produces a hash value z of fixed length.

  • Efficiency h(x) is relatively easy to compute.

  • 抗原像性 Preimage resistance：对于给定的输出z，不可能找到任何输入x使得h（x）= z，即h（x）是单向的计算。

    例子：Bob发送签名消息给Alice： kpr,B=d, kpub,B=e (e_k(x), sig_kpr,B(z)). e_k是双方的对称加密如AES密钥，然后Bob使用RSA进行签名，s=sig_kpr,B(z)) ≡ z^d mod n，任何人都可以通过Bob的公钥计算出哈希值 s^e ≡ z mod n.，如果hash function不是单向的，则任何人都可以反向计算出对应的消息x h⁻¹(z) = x.从而就绕过了双方的对称加密

  • 抗第二原像性 Second preimage resistance：给定x1，因此给定h（x1），通过计算找到任何x2使得h（x1）= h（x2）是不可行的。 根据pigeonhole principle或Dirichlet’s drawer principle这是不可能的，所以只能退而求其次我们要尽可能保证实践中无法构造出x2，意味着不存在analytical attack，至于避免爆破攻击（exhaustive brute force）我们可以增加哈希方法输出的长度。

  • 耐碰撞性 Collision resistance：通过计算找到任何一对值 x1≠x2使得h（x1）= h（x2）是不可行的（跟前面不同，这里是任意x1 x2而不是给定x1）

    This property is harder to achieve than weak collision resistance since an attacker has two degrees of freedom: Both messages can be altered to achieve similar hash values. We show now how Oscar could turn his ability to find collisions into an attack. He starts with two messages, for instance: x1 = Transfer $10 into Oscar’s account x2 = Transfer $10,000 into Oscar’s account He now alters x1 and x2 at “nonvisible” locations, e.g., he replaces spaces by tabs, adds spaces or return signs at the end of the message, etc.

    The most important consequence of the birthday attack is that the number of messages we need to hash to find a collision is roughly equal to the square root of the number of possible output values, i.e., about √2n = 2^n/2.

    Hash functions should have at least 160-bit output length in order to withstand collision attacks; 256 bit or more is desirable for long-term security. MD5, which was widely used, is insecure. Serious security weaknesses have been found in SHA-1, and the hash function should be phased out. The SHA-2 algorithms all appear to be secure. The ongoing SHA-3 competition will result in new standardized hash functions in a few years.

  除此之外，特别对于签名的有效性来说，还需要具备另外一个属性：找不到有效可行的方法来修改信息或哈希摘要以及签名，并且让修改后的新签名变成新消息的有效签名

• 真实性 authenticity

  某个签名必须只能是对应的私钥持有者签的名，所以通过签名可以认定其身份，使接收者非常有理由相信该消息是由已知的发件人创建的；

  反例：对称加密算法就不适用于签名，因为大家持有的是一样的密钥

• 不可否认性 Non-repudiation

  已对某些信息进行签名的有关方不能否认自己做过这个签名，当然其他人也不能仅通过访问公钥来伪造有效签名；

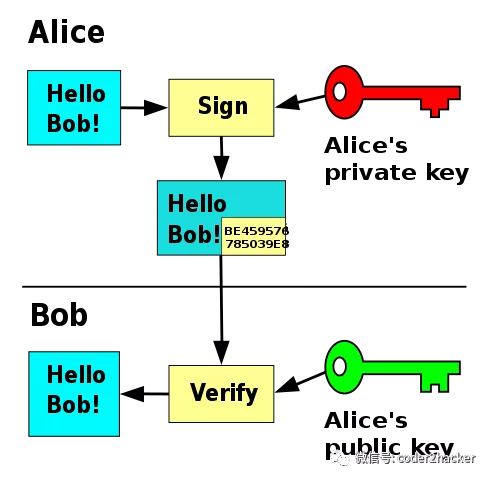
虽然不能篡改签名，但很多digital signature 算法都不能免疫于 forgery/replay attack 伪造攻击，因为当Alice做了足够的多的签名，黑客Craig可以从从选择某个签名和信息对，作为中间人replay发给Bob，所以签名只是一方面，整个程序的安全性还需要建立在整体的设计上，比如比特币就不会受到forgery attack的影响，如果受影响就相当于出现double spend，而这个正是比特币的设计所避免的。

Note: 关于哈希 Hash Function和MAC-message authentication codes

哈希方法 Hash Function是不带key的/keyless，常用于最重要的两个应用： 数字签名 和 MAC-message authentication codes，

digital signature VS Hmac

-	Hash	MAC(keyed hash function)	Digital signature
Integrity	Yes	Yes	Yes
Authentication	No	Yes	Yes
Non-repudiation	No	No	Yes
Kind of keys	None	Symmetric	Asymmetric

Message Authentication Code (MAC) 又称为keyed hash function以及cryptographic checksum

哈希方法length extension attack 长度延展攻击 像md5 sha1等基于 Merkle–Damgård construction 的哈希算法并不安全， 由此构造的MAC=》secret key prefix: BadMAC(secret,message)= H(secret ‖ message) is the concatenation of the Key and the Message.容易受到 length extension attack 长度延展攻击： https://en.wikipedia.org/wiki/Length_extension_attack https://www.bilibili.com/video/BV1uy4y1h7Qr/ https://crypto.stackexchange.com/questions/3978/understanding-the-length-extension-attack

secret key suffix 虽然没有延展性攻击，但是存在birthday attack

安全的MAC实现： HMAC_k(x) = h[(k'⊕opad)||h[(k'⊕ipad)||x]].

secret key suffix VS HMAC

However, the big advantage of HMAC over H(m||k) is that collision-resistance of the underlying hashing function is not needed. https://crypto.stackexchange.com/questions/5725/why-is-hmk-insecure My opinion: the biggest advantage of hmac construction is that the attacker can't compute hmac value without knowing the secret key while with H(m||s) attacker still can simply compute H(random messge) to find a collision(存在birthday attack)

RSA Signature

公钥加密，私钥解密反过来就是RSA的签名算法即：

私钥加密，公钥验证

P.S. 有意思的是RSA后两个字母刚好跟 Signatrue Algorithm缩写一样，但实际上是 Rivest–Shamir–Adleman 三位大佬姓氏的缩写

RSA安全性是基于大素数分解问题 Large Prime factorization

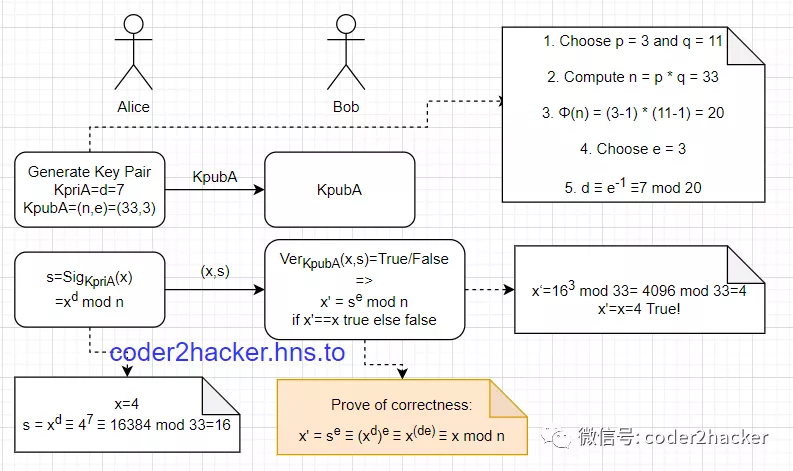
Elgamal Digital Signature

Elgamal signature

其安全性是基于离散对数问题 discrete logarithms

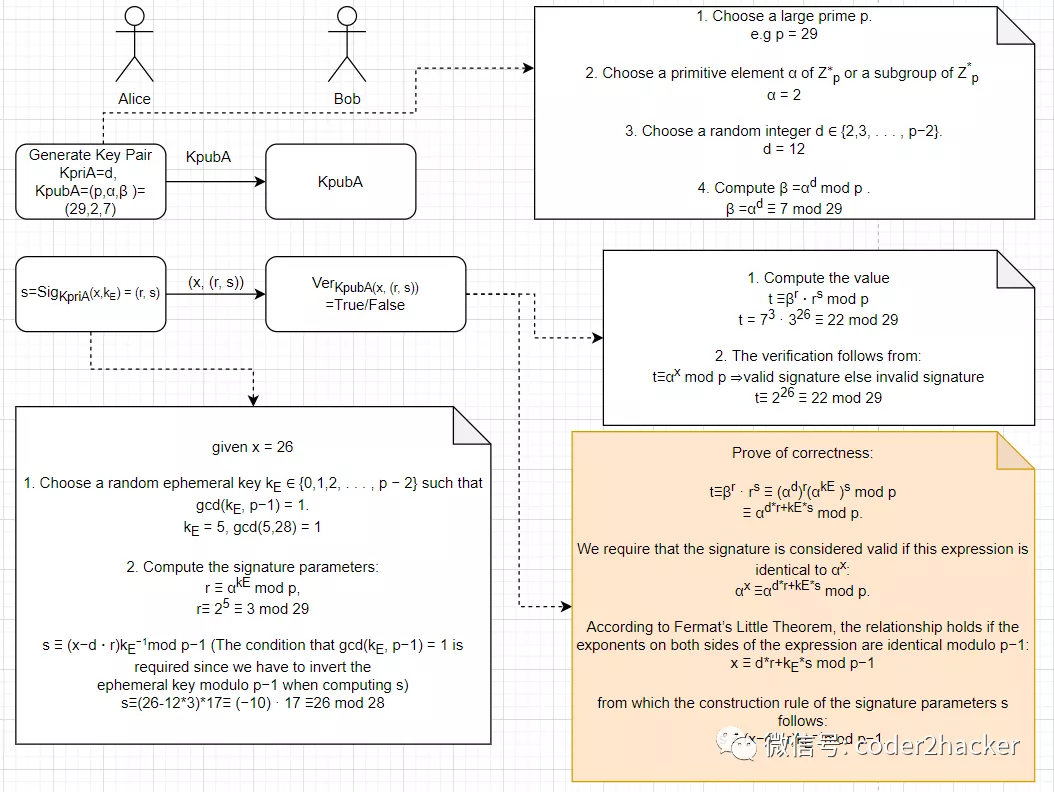
DSA - Digital Service Standards

正如其名字本身数字签名算法，这是由美国国家标准学会提议与技术National Institute of Standards and Technology （NIST）基于Elgamal signature scheme 提出的美国联邦政府数字标准签名Digital Service Standards (DSS)

签名只有320位，但是签名验证比RSA慢，因为是基于Elgamal signature scheme 所以其安全性也是基于离散对数问题 discrete logarithms

ECDSA - Elliptic Curve Digital Signature Algorithm

ECDSA secp256k1

keccak

secp256k1's elliptic curve y² = x³ + ax+b (a=0,b=7) over the real numbers: the graph is

secp256k1 is actually defined over the field: y² = x³+ax+b over Fp graph will in reality look like random scattered points...

https://github.com/bitcoinbook/bitcoinbook/blob/97df56f77c06813b1e028b5b1f2dbc036f27b1fc/ch04.asciidoc#L128 https://github.com/jimmysong/programmingbitcoin/blob/master/ch03.asciidoc

ECC位长度在160–256位的范围内, 其安全性与1024–3072位的RSA和DL相同，更短的位长，处理时间越短，并且签名也短，由于这些原因，1998年椭圆曲线数字签名算法（ECDSA）被ANSI 美国国家标准研究所进行了标准化。

ECDSA的构建步骤跟DSA很接近，但是其离散对数问题是构造在基于素数域Zp或者是伽罗华域 Galois fields GF(2^m) 的椭圆曲线上，所以在实际计算过程上完全跟DSA不同。

https://hackernoon.com/hacking-a-bitcoin-wallet-642u36sa

https://github.com/bitcoinbook/bitcoinbook/blob/db678d15c08e7be4180ba9e9fbc60ee004eb5c3c/ch06.asciidoc

https://www.mycryptopedia.com/public-key-private-key-explained/

Sig = Fsig(Fhash(m),dA)

dA is the signing private key

m is the transaction

Fhash is the hashing function

Fsig is the signing algorithm

Sig is the resulting signature

The signing function (Fsig) produces a signature (Sig) that comprises of two values: R and S:

Sig = (R, S)

Once R and S have been calculated, they are serialized into a byte stream that is encoded using an international standard encoding scheme that is known as the Distinguished Encoding Rules (or DER). In order to verify that the signature is valid, a signature verification algorithm is used. Verification of a digital signature requires the following:

Signature (R and S)

Transaction hash

The public key that corresponds to the private key that was used to create the signature

Verification of a signature effectively means that only the owner of the private key (that generated the public key) could have produced the signature on the transaction. The signature verification algorithm will return ‘TRUE’ if the signature is indeed valid.

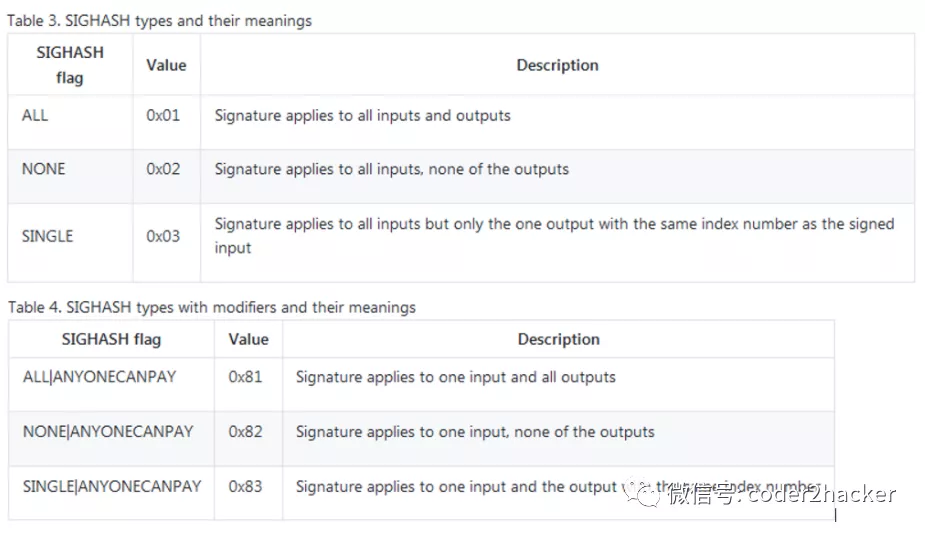
Sig = (R, S, SIGHASH) R and S are serialized into a byte-stream using an international standard encoding scheme called the Distinguished Encoding Rules, or DER. Signature Hash Types (SIGHASH): - ALL - NONE - SINGLE - ANYONECANPAY ECDSA Math AND The Importance of Randomness in Signatures If the same value k is used in the signing algorithm on two different transactions, the private key can be calculated and exposed to the world! To avoid this vulnerability, the industry best practice is to not generate k with a random-number generator seeded with entropy, but instead to use a deterministic-random process seeded with the transaction data itself. This ensures that each transaction produces a different k. The industry-standard algorithm for deterministic initialization of k is defined in RFC 6979, published by the Internet Engineering Task Force